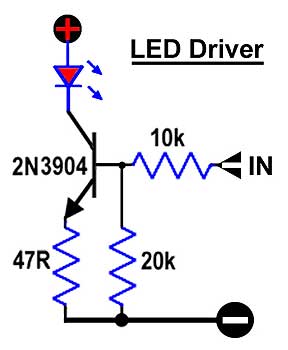
Figure 1: A positive moving input signal turns the transistor “on,” so the collector pulls the LED’s cathode toward ground via the 47-ohm resistor.
This month, “Tech’s Files” will stray from the conventional audio signal path and venture into some über-basic examples of analog control and display circuitry. All of us are familiar with LEDs as visual indicators. As I tell students in the classes I teach, Electronics 101 defines a diode as a device that allows current to flow in only one direction, which can enable rectification, commonly used to convert an alternating current into direct current. In the 1920s, diodes were found to emit light in certain applications. Years later, experiments with diodes made of exotic materials (such as silicon germanium and gallium arsenide phosphide) spawned commercial LEDs in various colors.
A single LED can translate amplitude variations into a corresponding brightness range — not very precise, but definitely operator-intuitive. An audio signal can drive an LED to moderate brightness, and by exploiting its ability to rectify an incoming signal, two LEDs in parallel with the signal path can create a simple fuzz box. If the design goal is to make the LED bright enough to get attention, then a transistor (or op amp) must be inserted between the LED and the audio signal to act as a buffer/driver.

Positive DC turns this transistor “on,” so the collector pulls the relay coil cathode toward ground via the emitter resistor.
Figure 1 shows a simple buffer/driver option. Swapping out the LED for a load resistor (on the collector) yields the more familiar single-stage voltage amplifier. Like a transistor, an LED is a semiconductor that has polarity and must be oriented accordingly. Notice that the LED “arrow” is pointing in the same direction as the NPN transistor’s emitter. This particular circuit is being used to indicate the threshold and degree of processing for a simple optical limiter.
Regardless of whatever “load” (a resistor, LED or relay coil, as shown in Fig. 2) is being used, the resulting headroom, LED brightness or reliable relay latching can easily be optimized if the user tweaks the bias resistor on the emitter and the voltage divider (the two resistors connected to the base).
Either/Or and Other Options
Before diving into relay-driving circuits, let’s review what switches do. Switches fall into many categories based on the number of circuits (poles) and the number of connections or positions. An old-fashioned power switch — toggle, rocker or push-and-latch type — is often single-pole/single-throw (SPST) or double-pole/single-throw (DPST). All of these types have a maximum of three positions (center OFF) and two “throws”; just think of Dr. Frankenstein “throwing” that giant switch lever.

A quad comparator drives this simple LED ladder. Three series resistors across the bottom set the threshold for each LED.
Whereas a single “throw” allows a single option — on or off, connect or disconnect, make or break — a two-throw switch allows an either/or option. Polarity-reverse switches are more likely to be double-pole/double-throw (DPDT). Toggle switches can typically have one to four poles, beyond which the physical size becomes unwieldy.
Rotary switches can have multiple poles and position/throws, and options like break-before-make (non-shorting) and “shorting” for jobs like input select or EQ boost/cut, respectively. Often, rotary switches (and pots) are customized (more costly), and sometimes they need to conserve front panel real estate or have remote-control capability, the latter being our focus.
Modern “soft” power switches — classified as “momentary” SPST — are at the front of more complex control circuitry that allows almost no current to pass when the mechanical switch is closed (conducting). Here, all the heavy work is done by “remote control,” using either electronic (FET) switching or relays. A relay is a switch mechanism with a magnetically conductive pole piece that can be opened or closed when a current is passed through a coil that, in turn, generates a magnetic field. (The coil is described as “energized.”)
A relay can be a single- or double-throw switch, with one, two or four poles being very typical. A single-pole/single-throw switch could control multiple relays; a single-pole/multiple position switch could select one relay from a group of several. There’s a relay flavor to suit any in a large variety of applications.
The coil in this telecommunications-grade relay draws about 11 mA, power consumption being critical if the relay is electronically controlled by a microprocessor or other integrated circuit. Conversely, switch mechanisms for high-voltage/high-current applications require greater distances between switch contacts (to prevent arcing) and higher tension to keep the contacts closed (and low-contact resistance); therefore, greater current is flowing in the relay coil to create a more substantive magnetic field. Here again, a transistor buffer driver can do the heavy lifting.
The coil driver detailed in Fig. 2 was used in a custom 5.1-channel mute box. Rather than drive all relays from a single switch, I isolated each relay from the master switch with a transistor, allowing future options such as individual mutes or linking to the existing monitor controller.
Look at Dem Lites!
While a single LED does a decent job of indicating level changes, a bar graph display can expand the resolution to provide as much precision as necessary. In this application, a simple Class-A DI/mic preamp, I wanted four LEDs to indicate signal presence at four levels starting at instrument level (-20 dBu), nominal (+4 dBu), followed by the highest clean level (+15 dBu) before going into soft clipping (+20 dBu). In class, a comparator was chosen to teach my students one of the ways to get the job done, the alternatives being a dedicated LED meter driver chip and the more challenging micro-controller, with the latter requiring programming skills.
The circuit is fairly simple if you look at one comparator at a time (see Fig. 3). The LM-339 is a 14-pin IC with four comparators, enough to drive four LEDs. A comparator is like an op amp configured for a differential (balanced) input signal, but instead of looking for balanced audio, one input sees the AC (audio) signal while the other sees one step in a DC voltage divider/ladder. When the audio signal crosses the DC threshold, the comparator output swings in the direction that turns the LED on.
In addition to the comparator is a PNP transistor current source. Note that the 2N3906 emitter arrow is opposite that of the 2N3904 in Fig. 1. Its job is to keep LED brightness constant, no matter how many LEDs are on. Similar to an op amp running on a single-voltage supply, the comparator is given a reference DC voltage via the trim pot. Once the ladder is optimized for each LED, the trim pot serves as an overall calibration control. In the classes I teach, each student calculates the steps in the voltage ladder, in both directions; each DC step roughly corresponds with the RMS voltages associated with the dBu levels.
Familiarity with schematics often expedites the design process. You’ll find lots of help from manufacturers’ data sheets and application notes at their respective Websites, as well as through parts dealers such as Digi-Key, Allied and Mouser. A Web search for a 2N3904 or an LM339 should put a manufacturer’s page at or near the top — look for National, Fairchild or ON semiconductor. Just beware the unscrupulous Website that asks you to pay for data sheets!
For more fun with Eddie Ciletti, visitwww.tangible-technology.com.




